Rebonds, poids apparent, satellite, associations de résistors, solénoïde, loupe : concours kiné Berck 2010

Rebonds d'une balle .
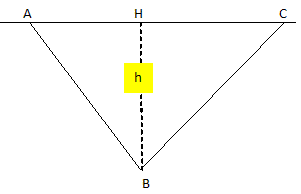
Une balle est lâchée sans vitesse initiale d'une hauteur h = 2,00 m par rapport au sol. 
Cette balle élastique effectue une succession de rebonds verticaux. 
L'énergie cinétique de la balle juste après un rebond diminue de 37 % par rapport à son énergie cinétique juste avant  ce rebond. 
On considère une caméra dont l'objectif est placé dans un plan horizontal situé à une hauteur h'=40,0 cm par rapport au sol. 
On néglige l'action de l'air sur la balle. 

Question : 

Déterminer le nombre de fois où la balle va passer dans le plan de l'objectif de la caméra. 
3, 5 ;

7 ;

9 ;
11 ;
aucune réponse exacte 



Poids apparent.
On dispose d'un ressort de masse négligeable, de constante de raideur  k = 5,4 N / m et de longueur à vide L₀ = 12 cm. L'extrémité supérieure est fixée à un support horizontal.
On suspend à l'extrémité inférieure de ce ressort une sphère métallique de rayon R = 1,5 cm. La longueur du ressort à l'équilibre est L₁ = 17 cm.
On immerge ensuite complètement  la sphère dans un liquide de densité d inconnue. La longueur du ressort à l'équilibre est L₂ = 15 cm.

Question : 

Calculer la densité du liquide.
 
0,62 ;

0,78 ;

0,85 ;
0,92 ;
0,98 ; 
aucune réponse exacte


Satellite.
Un satelitte de masse m= 530 kg décrit une trajectoire circulaire autour d'une planète de masse M.
Ce satellite se situe à une altitude de h =340 km par rapport à la surface de la planète.
La période de révolution du satellite est T = 1 h 34 min et sa vitesse vaut 7,13 km/s dans le référentiel planètocentrique.

Question : 

Parmi les affirmations suivantes, relatives à ce satellite, combien y en a t-il d'exactes ?
 
- Le rayon de la planète vaut R = 6,1 10³ km.
- la masse de la planète vaut M = 4,9 10²⁴ kg.
- la densité moyenne de la planète vaut d = 5,2.
- La force gravitationnelle exercée par la planète sur le satelitte a pour valeur F = 4,2 10³ N.
- Le satellite est soumis  à une accélération normale a_N =7,9 m s^-2.



Associations de résistors

Question : 

Déterminer U_BM en volt. 
2,0 ;
4,0 ;
6,0 ;
8,0 ;
16,0 ;
aucune réponse exacte



Solénoïde
On considère un solénoïde de longueur L = 60 cm dont l'axe est perpendiculaire à la direction de la composante horizontale B_H du champ magnétique terrestre. Une boussole est placée au centre du solénoïde.
Quand on fait circuler  un courant d'intensité constante I = 88 mA dans un sens donné, la direction de l'aiguille de la boussole fait un angle aigu a avec l'axe du solénoïde.
En inversant le sens du courant, l'aiguille de la boussole tourne de 151° par rapport à sa position précédente.

Question : 

Calculer le nombre de spires N de ce solénoïde.  
420 ;
450 ;
500 ;
520 ;
550 ;
aucune réponse exacte






La loupe
Un oeil normal voit tous les objets situés entre l'infini e la distance minimale de vision distincte D_m = 25 cm.
On utilise une loupe assimilée à une lentille mince convergente de vergence C = 6,0 dioptries.
Un observateur place son oeil " normal " au foyer image de la loupe.
Il regarde un objet AB, perpendiculaire  à l'axe principal de la loupe, le point A étant situé sur l'axe.
On note L la distance algébrisée entre le centre optique et A.
On notera L₁ la valeur que l'on doit donner  à L pour que l'image A' de A soit à l'infini.
On notera L₂ la valeur que l'on doit donner  à L pour que l'image A' de A soit située  à la distance minimale de vision distincte.
La latitude de mise au point de la loupe est L₂-L₁.

Question : 

Calculer la latitude de mise au point en cm. 

11 ;

14 ;

18 ;

20 ;

22 ;

aucune réponse exacte 

correction fixe
correction chimix

---

Radioactivité, pendule et projectile : concours kiné Berck 2010

Césium 137.
Le césium 137 subit une désintégration ß^- et le noyau fils est le baryum 137. 
Une source radioactive contient une masse m₀ =253 µg de césium 137 à la date t=0. 
On mesure l'activité de cette source à une date t₁ et on obtient la valeur A₁ = 5,67 10⁸ Bq.
On donne N_A = 6,02 10²³ mol^-1 ; 
masse molaire du césium 137 : M = 137 g/mol ; 
demi-vie du césium 137 : t_½ =30,17 années.

Question : Calculer la date t₁ en années. 
15,5 ;
17,8 ;
22,4 ;
25,6 ;
30,2 ;
aucune réponse exacte 





Fission de l'uranium 235
Dans un réacteur nucléaire, l'énergie est produite par la fission de l'uranium 235 sous le choc d'un neutron lent. Le combustible nucléaire utilisé est l'uranium naturel enrichi à 3,4 % en uranium 235 fissile.
Chaque fission d'un noyau d'uranium 235 libère en moyenne une énergie de 200 MeV.
Le rendement de la transformation de l'énergie nucléaire en énergie électrique est de 31 %.
Le réacteur consomme une masse m = 95,9 kg de combustible nucléaire en une journée.
On supposera que tous les noyaux d'uranium 235, contenus dans le combustible, subissent une fission.
On donne : 
masse molaire de l'uranium 235 : M = 235 g/mol ; 1 eV = 1,602 10^-19 J.
Question : Calculer la puissance électrique ( en GW) fournie par ce réacteur.
0,90 ;
0,92 ;
0,94 ;
0,96 ;
0,98 ; 
aucune réponse exacte 




Spectre d'émission
Le spectre d'émission de l'atome de sodium révèle la présence d'un doublet de raies jaunes de longueur d'onde l₁ =589,0 nm et l₂ = 589,6 nm.
Ces deux raies correspondent à une désexcitation de l'atome de sodium, à partir de deux niveaux d'énergie très proches, vers l'état fondamental.
Question : Déterminer l'écart d'énergie ( en meV ) entre ces deux niveaux.
1,2 ;
1,6 ;
2,1 ;
2,4 ;
2,5 ;
aucune réponse exacte


Balise.
Deux bateaux A et C sont séparés l'un de l'autre par une distance de 27 km et ils se trouvent dans le plan vertical contenant la balise.
Le bateau A capte le signal 7,7 s après son émission.
Le bateau C capte le signal de la balise 10,9 s après son émission.
Le son se propage à vitesse constante dans l'eau de mer  : v = 1,5 10³ m/s.
Question : Déterminer la profondeur h ( en km) à laquelle se trouve la balise.
2,3 ;
2,6 ;
2,9 ;
3,2 ;
3,5 ;
aucune réponse exacte

Pendule et projectile.
Masse de la spère : m = 250 g. On lâche la bille en A sans vitesse initiale. 
Quand la bille arrive en B, un dispositif spécifique la décroche du fil et elle continue son mouvement sous la seule action de son poids.
On note S le sommet de la trajectoire de la bille après son décrochage. 
On note P le point de contact avec le sol. 
On néglige l'action de l'air sur la bille dans toutes les phases du mouvement.
Coordonnées des points B et C : x_B =12,2 cm ; y_B =13,4 cm ; x_C =0 cm ; y_C =50,0 cm

Questions : 
Calculer la longueur L du fil constituant le pendule.
Calculer la vitesse en B, notée v_B ( m/s).

Calculer la tension T du fil en B.

Calculer l'ordonnée du sommet SCalculer l'abscisse du point P (en cm).


correction fixe
correction chimix

---

physique : électricité, oscillateur mécanique : Ceerrf 2010

Analyse dimensionnelle.
Une particule de masse m et de charge q est accélérée sous une tension électrique U. 
Elle est alors placée dans une région de l'espace où règne un champ magnétique B. 
La trajectoire de la particule est circulaire de rayon R = 1/ B (2mU/|q| )^½.
Question : 
En fonction des unités de base, la tension électrique U s'exprime en :
m² kg s^-3 A^-1 ;
m² kg² s^-3 A^-1 ;
m kg s^-3 A^-1 ;
m² kg s^-3 A^-2 ;
m² kg s^-2 A^-2 ;
aucune réponse exacte.





Dipole LC :
Un condensateur de capacité C = 0,10 µF est chargé sous une tension U =50V. On le déconnecte de ce générateur et on le relie à la date t=0 à une bobine idéale d'inductance L = 100 mH.
Question : 
On peut affirmer que :
A- On observe des oscillations électriques libres non amorties. 
B- La fréquence propre des oscillations est de l'ordre de 1,7 kHz.
C- L'énergie stockée par le condensateur en fin de charge est 12,5 µJ. 
D- A la date t=0⁺, l'intensité dans le circuit est maximale. 
E- Dans le circuit LC, la charge à pour expression q(t) = U cos((LC)^-½t). 


Dipole électrique linéaire.
La caractéristique intensité tension d'un dipole électrique linéaire passe par
les deux points de fonctionnement A ( 300 mA ; 14 V) et B ( 1,5 A ; 2,0 V).
Question : 
On peut affirmer que :
A- ce dipole est à classer dans la catégorie des récepteurs.
B- La loi de fonctionnement de ce dipole est de la forme I = a U + b avec a>0 et b>0.
C- Lorsqu'il fonctionne au maximum de sa puissance ce dipole délivre une intensité de 850  mA.
D- Si U = 10 V alors I = 1,0 A.
E- Ce dipole dissipe par effet joule, une puissance du type rI²t.


Charge d'un condensateur à intensité constante.
Le condensateur initialement déchargé est chargé à intensité constante I= 10 µA.
Question : 
On peut affirmer que :
A- La tension aux bornes du condensateur a pour expression u(t) = E(1-exp(-t/t)). 
B- Les armatures du condensateur chargé portent des charges de mêmes valeur.
C- Si au bout de 10 s, u(t) = 20 V alors C = 5,0 µF.
D- Si on double le temps de charge, la tension aux bornes du condensateur double.
E- Si on double le temps de charge, l'énergie stockée dans le condensateur double.


Oscillateur élastique horizontal sinusoïdal.
Pulsation w = 1,0 rad/s.
Quand x = 1,0 cm on mesure une vitesse v_x =3,0 cm/s.
Question : 
Evaluer l'amplitude X_m ( cm) du mouvement :
7,6 ;
6,5 ;
5,4 ;
4,3 ;
3,2 



correction fixe 

correction chimix 

---

Lentille mince equiconvexe :Ceerrf 2010

Question : On considère une lentille mince convergente de distance focale f' inconnue.
-Faire le schéma avec la lentille, un objet AB situé à gauche de la lentille ( AO = 1,5 f')  et l'image A'B'. 
Justifier le tracé de trois rayons.
-Retrouver les formules du grandissement et de conjugaison de Descartes.



Question : A l'aide d'un banc d'optique, d'un objet représenté par une lettre d, de la lentille précédente et d'un écran, on a obtenu la série de mesures suivantes :
(La mesure algébrique de OA est notée p ; la mesure algébrique de OA' est notée p'.)

p (cm)	-100	-60	-50	-40	-35	-30	-25	+20	30	50
p'(cm)	11,1	12,0	12,5	13,3	14,0	15,0	16,7	6,7	7,5	8,3

-Pour plusieurs des mesures précédentes,il a fallu une lentille auxiliaire. Lesquelles et pourquoi ?

Question :  Deux points sont représentés sur cette courbe avec leurs coordonnées.

-Cette courbe est-elle en accord avec la loi de conjugaison de Descartes ? Justifier.
-Déterminer à partir de la courbe la vergence puis la distance focale de la lentille.


Question :  
Cette lentille est équiconvexe.
La forme est-elle cohérente avec la nature de cette lentille ?




Question : 

La vergence d'une lentille mince peut se calculer en appliquant la formule suivante :
Les grandeurs écrites en bleu et en gras sont algébriques.
C = (n-1) [1/ S₁C₁ -1/S₂C₂] 
où n est l'indice de réfraction du milieu transparent constituant la lentille et SC le rayon de courbure des dioptres d'entrée ou de sortie de la lentille.



-Déterminer S₁C₁ et S₂C₂ pour la lentille, sachant que le milieu transparent est du verre d'indice n=1,5.



Question : Un objectif photographique est assimilé à la lentille convergent L.

-Déterminer l'expression et la valeur numérique de la hauteur H' sur la pellicule d'un arbre de hauteur H = 15 m, situé à une distance d = 50 m de la face d'entrée de l'objectif.
-Indiquer quel est l'encombrement minimal ( distance  entre la face d'entrée de l'objectif et la pellicule) du dispositif dans ces conditions.





correction chimix 
correction fixe 

---

Projectile, satellite, pendule, ondes : EFOM 2010

Question Vrai/faux : 
Projectile.
On dlance un projectile G considéré comme ponctuel, à partir d'un point A, avec une vitesse initiale v0 faisant un angle a avec l'horizontale. On néglige les frottements.
h = 3,00 m ; y_S = 4,50 m ; x_P = 10,5 m.

A- Les équations horaires de la position G sont :
x = v₀ sin a t et y = -½gt² + v₀ cos a t +h.
B-  L'équation de la trajectoire de G est : y = -½gx² / (v₀cos a)² +x tan a + h.
C- La composante de la vitesse de G selon l'axe vertical au point S est nulle. 
D- La vitesse de G reste constante. 
E- Aucune de ces propositions n'est exacte. 

Question Vrai/faux :  Satellite.
On considère la terre de masse M de rayon R et un de ses satellites de masse m. le satellite gravite autour de la terre avec une période T. Il est situé à une distance h de sa surface. 
Les frottements de l'air sont négligeables et R ~ 6700 km.
A-La norme de la force d'attraction F exercée par la terre sur m s'exprimme par F = GMm / h².  
B- La masse de la terre est environ M = 6,7 10²⁴ kg. 
C- La masse de la terre est environ M = 6,0 10²⁴ kg.
D- La troisième loi de Kepler s'écrit :  T²/r³ = 4 pi² / (GM) avec r = R+h. 
E- La troisième loi de Kepler s'écrit :  T²/r³ = 4 pi / (GM).  

Question Vrai/faux :  Oscillateur mécanique.
Soit un oscillateur mécanique ( solide-ressort horizontal) évoluant sans frottement. Soit m la masse du solide et k la constante de raideur du ressort. A t=0, le ressort est étiré. Son allongement est x₀ >0. On lance alors le solide avec une vitese v₀, horizontale dirigée vers la gauche.
A- L'énergie mécanique initiale du système est E_m = ½kx²₀. 
B-  A une date t >0, l'énergie mécanique du système se conserve car aucune autre force que la force de rappel du ressort ne  travaille. 
C-Le travail mécanique élémentaire de la force de rappel du ressort est le produit scalaire de deux vecteurs.
D-L'énergie mécanique du système est égale à la somme des travaux mécaniques des forces qui lui sont appliquées.
E-On introduit un dispositif qui crée des  forces de frottement. l'énergie mécanique du système augmente alors car la force de frottement s'exerçant sur le solide s'oppose au mouvement de ce dernier.
L'énergie mécanique diminue du travail des frottements.

Question Vrai/faux : 
Onde sonore basse fréquence. 
On utilise un stimulateur émettant une onde sonore à basse fréquence pour décontracter un muscle. L'onde émise est supposée longitudinale, progressive et périodique.
A- L'onde se propage avec un déplacement de matière perpendiculairement  à sa direction de propagation.
B- L''onde est caractérisée par sa double périodicité. 
C-L'onde voit sa célérité varier en fonction des milieux traversés. 
D- Il n'y a aucun transport de matière lors du passage de l'onde.
E- Toutes ces affirmations sont vraies.
A- 0,040 m.
B- 40 m.
C- 0,40 m.
D- 4,0 m. 
E- 2,0 m.

Question Vrai/faux : 
Pendule.
 Un objet sphérique de masse m = 100 g , relié à un fil inextensible, est lâché sans vitesse initiale en I. Il remonte jusqu'n J en suivant le parcours figuré ci-dessous. q₁ = 60°. 
Le fil mesure L = 1,8 m et OT = 80 cm. 
On suppose qu'il n'y a aucune perte d'énergie en passant en T et qu'il n'y a aucun frottement.

Parmi les propositions suivantes, quelle(s) affirmation(s) est (sont) vraie(s) ?
A. q₂ = 60 °. 
B. cos q₂ = -0,10, la bille passe au dessus de O.
C. q₂ = 30 °.
D. cos q₂ = 0,10.
E. Aucune de ces réponse n'est vraie.


Question Vrai/faux :  Pendule.
On considère un pendule formé d'une bille, assimilée à une masse ponctuelle m de centre d'inertie G, suspendue à un fil de masse négligeable de longueur L, fixé en un point J. A l'équilibre, la bille est en A à l'altitude zéro. On déplace G d'un angle a, le fil restant tendu. L'altitude de G est égale à h <0.
A- la période propre d'oscillations du pendule est T₀ = 2 pi ( g/L)^½.
B- La différence d'altitude h entre G et A s'exprime par : h = L(1-tan a). 
 C- L'énergie mécanique  de m est : E_m = mgL +½mv². F
D- la période propre d'oscillations du pendule est T₀ = 2 pi ( h / (g(1-cosa)))^½.
E- La période d'oscillation est assimilable à la période propre pout toute valeur de l'amplitude des oscillations. 


Question Vrai/faux :  Accellération d'un tracteur.
Un tracteur parcourt 900 m en 1 min 40 s, départ arrêté. 
Son accélération supposée constante vaut ( en m s^-2) :
A- 1,8. 

B- 3,6.  
C- 0,18. 
D-  18.  
E- 9,0.  


Question Vrai/faux :  Onde.
Soit une onde de fréquence f et de longueur d'onde l. Sa célérité est c₀.
A- La célérité  d'une onde mécanique est proportionnelle à l'amplitude de la pertutbation. 
B-  La relation qui lie les grandeur est l  = f/c₀. 
C- On observe sur l'écran, situé à une distance D, une figure de diffraction verticale.  
D- La tache centrale de diffraction observée possède une largeur L = 2lD/a. 

F- Une lumière polychromatique est une onde composée de radiations de plusieurs couleurs.


Question Vrai/faux :  Descente d'une luge.
On schématise ci-dessous le trajet d'une luge, supposée ponctuelle et de masse m = 1,0 kg, lâchée sans vitesse initiale à partir du point A. On donne h = 500 m et on néglige les frottements.

A- La vitesse en B est 10 m/s.
B-  On a alors -v²/r = -R +mgcosq et ma_T = -mg sin q où v est la vitesse de m.
C- le théorème de l'énergie cinétique permet d'écrire : ½mv² -½mv²_B = - mgr ( 1-cosq).
D-La norme de R est : R = 2mgh/r +mg (3 cos q-2). 
F- Le poids du mobile est une force dite conservative.


Question Vrai/faux :  Une source monochromatique émet une radiation de longueur d'onde l = 6,00 10⁵ pm dans le vide. Sa puissance est de 0,600 mW. A sa sortie, le faisceau a un diamètre d = 2,00 mm et il a un demi-angle de divergence de 1,00 mrad.
A. La puissance lumineuse  émise est d'environ 10,0 W m^-2.
B. La puissance lumineuse  émise est d'environ 200 W m^-2. 
C. La puissance lumineuse  émise est d'environ 1000 W m^-2.

On place un écran situé à L =2,00 m de la source.
D. La puissance lumineuse reçue par l'écran est d'environ 200 W m^-2. 
F. La puissance lumineuse reçue par l'écran est d'environ 1000 W m^-2. 


correction fixe 
correction chimix

---

Dipole RC EFOM 2010

Dipole RC.
On monte en série un générateur de fem E = 5,0 V, un conducteur ohmique de résistance R = 50 ohms, in condensateur de capacité C =30 µF et un interrupteur ouvert. A t=0, on ferme l'interrupteur.
A- la constante de temps du dipole est 1/RC.
B- cette constante vaut 1,5 ms.
 C- cette constante vaut 15 ms.
D- cette constante vaut 3,0 ms.  
E- A valeur de R constante, plus on augmente la valeur de C, plus la durée de la charge complète du condensateur diminue. 


La constante de temps t de la charge d'un condensateur, dont la tension aux bornes est u_C(t) peut être déterminée de la façon suivante :
A-A partir de la solution de l'équation différentielle u_c(t) = E/R exp(-t/t).
B- Graphiquement en déterminant l'abscisse de l'intersection entre la tangente en zéro à la courbe u_c(t) et l'asymptote u_c(oo) =E. 
C- D'après l'observation des oscillations d'u_c(t), on accepte que le régime permanent est atteint au bout de t. 
D- D'après l'observation des oscillations d'u_c(t), 
le condensateur est chargé à 63 % après un temps égal à ½ t.  
E- Aucune de ces méthodes n'est acceptable.
correction fixe
correction chimix

---

acide base, conductimétrie, oxydoréduction, chimie organique : EFOM 2010

QCM VRAI/FAUX

Pile.
On étudie la pile formée par les couples Zn²⁺/Zn et Cu²⁺/Cu.
A- Il s'agit de la pile de de Volta.
B-  Il s'agit de la pile Danielle.
C- Il y a oxydation au pole positif.
D- On note conventionnellement cette pile :  Zn²⁺aq |Zn(s) || Cu²⁺aq| Cu(s).
E- Le symbole || indique la séparation entre les demi-piles qui est une condition nécessaire à la naissance du courant. 

pKa et force d'un acide.
A- Un acide faible est d'autant plus fort que le pKa du couple auquel il appartient est élevé.
B-  Plus le pKa d'un couple acide / base est petit, plus l'acide du couple est dissocié dans l'eau, à concentration apportée égale.
C- Plus un acide faible est dilué, plus il a tendance à être fort.
D- La dilution n'a aucune influence sur la dissociation d'un acide AH dans l'eau.
E- Lorqu'un acide est faible dans l'eau, sa base conjuguée est forte dans l'eau.  


Conductivité.
On connaît les conductivités molaires dans les conditions standards de différentes solutions :
 L_NaCl = 126 10^-4 S m² mol^-1 ; L_HCl = 425 10^-4 S m² mol^-1 ; L_H2SO4 = 860 10^-4 S m² mol^-1 ;
A- la conductivité de la solution d'acide sulfurique est bien plus grande que les autres valeurs car c'est un diacide.
B-  Pour les conductivités molaires ioniques, on a la relation : l_{H+ aq} < l_{Na+ aq} . 
C- L_Na2SO4 = 687 10^-4 S m² mol^-1.
D- L_Na2SO4 = 262 10^-4 S m² mol^-1.
E- La conductivité molaire standard L_Na2SO4 ne vaut aucune des valeurs précédentes

Oxydation ménagée  par l'ion permanganate de monoalcools.
A- Tous les alcools sont oxydés.
B- Les alcools tertaires sont oxydés en acide carboxylique.
C- Les alcools primaires s'oxydent tous en aldehydes.
D- Les alcools secondaires s'oxydent en cétone.
E- Toutes les réponses précédentes sont fausses. 

titrage acide base (soude).
Une prise d'essai de volume V₀ d'une solution d'un monoacide fort AH de concentration en acide apportée c₀ est titrée par une solution de soude de concentration c₁.
On exprime le volume de soude versé par la valeur V et on pose x= V / V_E où V_E est le volume de soude versé à l'équivalence.
A- On peut définir l'équivalence du titrage par x =c₁V/ ( V₀c₀)=1 .
B- La concentration en A^- initialement présente vaut : [A^-aq]_i =V₀c₀/ V.
C- Avant l'équivalence, la concentration en ions oxonium restants est : [H₃O⁺aq] =V₀c₀(1-x)/ (V+V₀) .
D- Le meilleur indicateur coloré pour ce titrage est la phénolphtaléine.
E- A l'équivalence du titrage  [H₃O⁺aq]_équi = 1,0 10^-6 mol/L.


Solubilité du chlorure de plomb PbCl₂.
La solubilité du chlorure de plomb est  s = 5,00 mol/L à 25°C. La constante d'équilibre K associée à la réaction de solubilisation du chlorure de plomb vaut :

1,00 105 ;
125 ;
500 ;
20,0 ;
Est-il possible de diminuer  les concentrations des espèces en solution saturée en modifiant la température de la solution. 




Acide acétique.
On prépare une solution S d'acide acétique de conductivité s = 0,020 S m^-1
et de concentration en soluté apportée c₁ = 2,0 10^-2 mol/L.
l_H3O+ = 35 10^-3 S m² mol^-1 ;  
l_CH3-COO- = 5,0 10^-3 S m² mol^-1 ;
 A- Cette réaction est limitée et [CH₃COO^-]_éq = 0,50 mol m^-3.  
B-  Cette réaction est limitée et [CH₃COO^-]_éq = 500 mol dm^-3.
C- la constante d'équilibre associée à la réaction de l'acide acétique sur l'eau vaut K = 12,5.
D- la constante d'équilibre associée à la réaction de l'acide acétique sur l'eau vaut K =12,5 10^-6.
E- La conductivité de la solution S dépend fortement de sa température.

 Les corps gras.

A- Ils répondent à la formule générale suivante, où R, R', R" désignent des chaînes carbonées. 

B- sont des triesters.
C- sont des produits de la saponification.
D- sont des triglycérides.
E- ont la propriété d'être des acides. 


Evolution spontanée d'une réaction chimique.
Soit une réaction de quotient de réaction Q_r et de constante d'équilibre K.
A- l'équation chimique s'écrit obligatoirement avec un signe = 
B- le système chimique n'évolue pas si Q_r < K. 
évolution dans le sens direct.
C- le système chimique  évolue dans le sens direct de l'écriture de la réaction si Q_r < K. 
évolution dans le sens indirect.
D- le système chimique peut évoluer vers l'équilibre et la réaction chimique être athermique.
E- le système chimique ne peut évoluer que dans le sens d'une réaction exothermique.


Titrage acide base.
L'équation chimique support du titrage par la soude d'une solution d'un acide AH se dissociant totalement dans l'eau est :
A- AH aq + HO^-aq = A^-aq + H₂O(l).
B-  H₃O⁺aq + HO^-aq =2H₂O(l).  
C- AH aq + B^-aq = A^-aq + BH(aq).
D- Un titrage équivaut-il à un dosage?
F- Un titrage est-il une technique de dosage?

Soit la réaction : 2H₂O(l) =H₃O⁺aq + HO^-aq :
A- elle n'a lieu que dans l'eau pure.
B-  elle correspond à la dismutation de l'eau.  
C- elle prouve que l'eau est de la famille des ampholytes.
D- elle permet de calculer le pH de neutralité de l'eau pure en fonction de la température.
F- toutes ces affirmations sont fausses.

A- un alcool tertiaire se caractérise avec le bleu de bromothymol.  
B-  le 2,3-diméthylbutanal a pour formule C₆H₁₂O. 
C- le 2-méthylpropanal et la butanone sont isomères.
D- la 2,4-DNPH réagit avec une cétone.
F- un alcool primaire et un alcool tertiaire peuvent être isomères.

L'ion benzoate est une base faible.
C₆H₅COO^- aq + H₂O(l) = C₆H₅COOH aq + HO^-aq.
A-La constante d'équilibre s'écrit : K =[C₆H₅COOH aq]_éq [HO^-aq]_éq / [C₆H₅COO^- aq]_éq .
B-  le quotient de réaction associé à la réaction précédente est nul à l'équilibre.  
C- K augmente.
D- on déplace l'équilibre dans le sens indirect.
F-On modifie la température : K reste inchangé.


correction chimix 

correction fixe 

---