QCM mécanique : Archimède, pendule, Kepler, moteur électrique( Kiné Berck 2009)

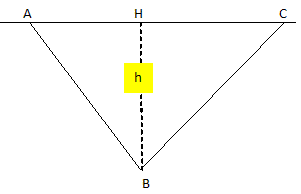
Question : 

Un solide de masse M_A est posé sur une table horizontale.
Il est relié par l'intermédiaire d'un fil inextensible et de masse négligeable à un solide B de masse M_B.

Le solide B lâché sans vitesse initiale entraîne le solide A.
On suppose que le fil reste toujours tendu et que tous les frottements sont négligeables.
On admettra que la tenion du fil a même valeur sur chaque brin de part et d'autre de la poulie.

M_A = 8,0 kg ; M_B = 3,5 kg ; g = 9,81 m s-2.

Déterminer la valeur de la tension du fil ( en N)

A	B	C	D	E	F
4,0	24	27	32	61	aucune réponse exacte

Question : 

Un cube de bois de côté a = 8,0 cm est relié à une sphère de rayon r = 1,0 cm par un fil inextensible de masse négligeable. 
Le système est plongé dans l'eau de mer. 
A l'équilibre le cube émerge d'une hauteur h. 
On ne tient pas compte de l'action de l'air sur la partie émergée du cube.  
On donne r_bois = 7,40 10² kg m^-3 ; r_acier = 7,80 10³ kg m^-3 ; r_{eau mer} = 1,03 10³ kg m^-3 ; 

Déterminer la hauteur h ( en cm).

A	B	C	D	E	F
1,2	1,5	1,8	2,1	2,3	autre

Question : 

pendule
On considère une table inclinée d'un angle a sur l'horizontale.
Un petit mobile autoporteur de masse m = 135 g est suspendu à u point fixe M par un fil inextensible de masse négligeable dont la longuer est L = 38,2 cm.
On néglige les frottements.
La période des oscillations de faible amplitude de ce pendule est :
T = 2 π [L / (g sin a )]^½.
On veut que la période T de ce pendule soit égale à la période des oscillations non amorties et de faible amplitude d'un pendule simple de même longueur L qui oscillerait à la surface de Mars.
Masse de Mars M = 6,42 10²³ kg ; rayon de Mars : R = 3,4 10³ km ; G = 6,67 10^-11 SI.
Calculer a en degré

A	B	C	D	E	F
22	27	32	36	38	autre

Question : 

On considère que les orbites de Vénus et de la Terre sont des cercles dans le référentiel héliocentrique. 
La période de révolution de Vénus est de 224,7 jours.
Le rayon de l'orbite de la terre est 1,50 10⁸ km, ce qui correspond à 1 U.A.
Calculer le rayon de l'orbite de Vénus ( en U.A).

A	B	C	D	E	F
0,46	0,52	0,61	0,66	0,72	autre

Question : 

Moteur électrique.
Un moteur est branché à une pile de fem E = 6,0 V et de résistance interne r = 1,2 ohms.
Le générateur fourni une puissance électrique de 2,8 W au moteur qui en convertit 80 % en énergie mécanique.
Déterminer la résistance électrique ( ohms) du moteur.

A	B	C	D	E	F
2,1	4,2	6,7	8,2	9,8	autre

chimix
correction fixe

---

condensateur : capteur de sonde d'humidité ( Kiné Berck 2009)

Le pourcentage d'humidité relative P de l'air est le rapport exprimé en pourcentage, de la quantité de vapeur d'eau contenue dans un certain volume d'air à la quantité correspondant à la saturation dans les conditions considérées.

L'air parfaitement sec a un pourcentage d'humidité relative P = 0%
et l'air complètement saturé d'humidité P = 100 %.

Le capteur de certaine sonde d'humidité est composé d'un condensateur plan dont la capacité C varie en fonction de ce pourcentage d'humidité relative.

On dispose d'un condensateur de ce type dont les caractéristiques sont données :

- la capacité est une fonction affine du pourcentage d'humidité relative P

- gamme d'utilisation : 10 %‹P‹90% ; sensibilité du capteur s = dC/dP. On réalise le circuit ci-dessous :

étape 1 : l'interrupteur K est en position 1 pendant le temps nécessaire pour que le condensateur se charge complètement. 
étape 2 : on bascule l'interrupteur en position 2.
Le circuit est le siège d'oscillations électriques libres et d'amortissement négligeable.
On suit alors l'évolution de l'intensité i dans le circuit.
On détermine la fréquence f des oscillations et la valeur maximale de l'intensité I_max.
On réalise une première mesure et on trouve I_max = 14,2 mA ; f = 1,12 kHz avec E = 12,0 V.

Questions : 
Déterminer la capacité C₁ (en nF) du condensateur lors de cette mesure.

En déduire la valeur de l'inductance L de la bobine.


On considère que l'inductance est constante au cours des mesures réalisées.

On effectue les mesures suivantes dans les mêmes conditions de température et de pression que la première mesure. le pourcentage d'humidité est lu sur un hygromètre.

Mesure	P ( %)	Imax( mA)	f(kHz)
n°2	30,4	13,7	1,16
n°3	54,8	14,9	1,07

La capacité C du condensateur varie en fonction de P selon la relation : C = aP+b
où a et b sont des constantes.
C est en nF et P en %.

Questions :
Déterminer les valeurs des constantes a et b.

En déduire la valeur de la sensibilité s ( en nF / %) du condensateur.


Déterminer la valeur P₁ du pourcentage d'humidité lors de la première mesure.





On injecte 5,0 mL d'une solution contenant une substance radioactive d'activité A₀ = 185 kBq dans le corps d'un chien endormi. 20 heures après l'injection, on effectue un prélevement de 25 mL de sang. La mesure de l'activité donne : A = 1,14 kBq.
On suppose que la substance radioactive est diffusée de manière homogène dans tout le sang de l'animal.
Demi-vie de la substance t_½ = 15 h.
Calculer le volume total ( en L) de sang dans le corps du chien.

A	B	C	D	E	F
1,0	1,2	1,4	1,6	1,8	autre

On considère un noyau de lithium ⁷₃Li dont la masse vaut m_Li = 7,0144 u.
1 u = 1,66054 10^-27 kg ; masse du neutron m_n=1,00866 u ; masse du proton m_p=1,00728 u ;
1 eV = 1,6022 10^-19 J ; c = 2,9979 10⁸ m/s.
Combien y a-t-il de propositions exactes ?

A- la masse de ce noyau est supérieure à la somme des masses des nucléons qui le constituent. 
B- le défaut de masse de ce noyau est 6,9876 10^-28 kg. 
C- le défaut de masse peut s'exprimer en MeV/c². 
D- l'énergie de liaison par nucléon de ce noyau est 5,60 MeV/nucléon. 
E- le noyau de lithium peut s'unir avec un autre noyau léger pour former un noyau plus lourd : il s'agit de la fission nucléaire. 



correction fixe
correction chimix

---

Chute d'une bille dans la glycérine ( Kiné Berck 2009)

Une bille sphérique en acier, de rayon r est lâchée sans vitesse initiale dans une éprouvette contenant de la glycérine. 
Lorsque la bille passe devant le repère n°1 elle a déja atteint sa vitesse limite de chute v_l.
Une caméra couplée à un ordinateur permet de mesurer la durée de la chute de la bille entre les deux repères.
Le début de cette mesure commence lorsque le bas de la bille est tangent au trait du repère 1 et s'arrête lorsque le bas de la bille est tangent au trait repère 2.
la durée de la chute de la bille entre les deux traits est notée Dt.
On réalise deux mesures de temps de chute en prenant la glycérine à deux températures différentes :
- pour q₁ = 15,0°C on trouve D t₁ =20,9 s
- pour q₂ = 20,0°C on trouve D t₂ =13,3 s

Les grandeurs écrites en gras et en bleu sont des vecteurs.  
Au cours de la chute la bille est soumise aux forces suivantes :
- son poids P, la poussée d'Archimède F exercée par la glycérine, la force de frottement fluide modélisée par
f = -kv avec k = 6prh ( h viscosité dynamique de la glycérine en Pa s).
Données : h = 80,0 cm ; r = 2,50 mm
masse volumique de l'acier r_a =7,85 g cm^-3 ; masse volumique de la glycérine r_g =1,29 g cm^-3 . 



Représenter sur un schéma les forces qui s'exercent sur la bille lors de la chute

Donner l'expression de la vitesse limite en fonction de h et Dt.


Etablir l'expression de la viscosité dynamique en fonction de g, r, h, Dt, r_a et r_g

Calculer les valeurs de la viscosité dynamique aux deux températures 15 °C et 20 °C. 


La viscosité dynamique dépend de la température et vérifie ,dans les conditions de cette expérience, la loi de Guzman-Andrade qui s'écrit :
h = A exp(B/T) avec A et B deux constantes à déterminer et T la température en kelvin. 

Déterminer la viscosité dynamique h₃ à 30,0°C.


En déduire la durée de la chute à cette température.


correction Chimix
correction fixe

---

acide base, oxydo-réduction, composés oxygénés, constante d'équilibre( Kiné Berck 2009)

Question : On dissout 7,2 g de benzoate de sodium C₆H₅COONa dans 250 mL d'eau distillée. 
On verse dans un becher 75 mL de la solution précédente et 25 mL d'acide chlorhydrique 
de concentration c= 0,050 mol/L. 
On ne tient pas compte de la réaction des ions benzoate avec l'eau.
Couple acide base : C₆H₅COOH / C₆H₅COO^- pK_a = 4,2.
 masses molaires : C : 12 ; H : 1 ; O : 16 ; Na : 23 g/mol.
Calculer le pH de la solution dans le becher

4,2
4,8
5,2
5,6
6,1
aucune réponse exacte

Question : 

Un échantillon de 1,20 g d'un mélange de poudre de fer et d'aluminium est traité par une solution d'acide chlorhydrique en excès. 
Après la réaction totale des deux métaux, il s'est formé un volume de 710 mL de dihydrogène. 
V_m = 24,0 L/mol.
Couples oxydant / réducteur : Fe²⁺ aq / Fe(s) ; Al³⁺aq /Al(s) ; H₃O⁺aq/H₂(g).
Calculer le pourcentage massique en fer dans le mélange.

42
48
51
65
82
autre

Question : chimie organique
Un composé organique A est composé de carbone, hydrogène et oxygène.A est un monoalcool et sa chaîne carbonée est saturée.
Le pourcentage massique en carbone est 64,9 %.
La combustion complète de 1,00 g de A conduit à la formation de 1,21 g d'eau.
Masse de Mars M = 6,42 10²³ kg ; rayon de Mars : R = 3,4 10³ km ; G = 6,67 10^-11 SI.
Calculer la masse molaire (g/mol) de ce composé.


32
46
60
74
90
autre

Question : Combien y a-t-il de propositions exactes ?

A- le test positif avec la 2,4-DNPH est caractérisé par la formation d'un précipité jaune orangé. 
B- le composé B possède un groupe carbonyle. 
C- le nom du composé B est la propanone. 
D- le composé A est un alcool secondaire. 
E- le composé A est le propan-2-ol. 

Question : Nitrate de plomb.
On prépare une solution de nitrate de plomb en dissolvant 50,0 g de solide Pb(NO₃)₂ dans de l'eau distillée pour obtenir 75,0 mL de solution. L'équation de la réaction de dissolution s'écrit :
Pb(NO₃)₂ (s) = Pb²⁺aq + 2NO₃^-aq.
Il n'est pas possible de dissoudre la totalité du solide. 
On filtre la solution préparée et on mesure la masse du solide non dissous : on trouve 10,6 g. 
Toutes les manipulations ont été effectuées à 20 °C.

Calculer la valeur de la constante d'équilibre associée à la réaction de dissolution du nitrate de plomb à 20 °C.

16
24
32
38
48
autre


correction chimix
correction fixe

---

Rebonds, poids apparent, satellite, associations de résistors, solénoïde, loupe : concours kiné Berck 2010

Rebonds d'une balle .
Une balle est lâchée sans vitesse initiale d'une hauteur h = 2,00 m par rapport au sol. 
Cette balle élastique effectue une succession de rebonds verticaux. 
L'énergie cinétique de la balle juste après un rebond diminue de 37 % par rapport à son énergie cinétique juste avant  ce rebond. 
On considère une caméra dont l'objectif est placé dans un plan horizontal situé à une hauteur h'=40,0 cm par rapport au sol. 
On néglige l'action de l'air sur la balle. 

Question : 

Déterminer le nombre de fois où la balle va passer dans le plan de l'objectif de la caméra. 
3, 5 ;

7 ;

9 ;
11 ;
aucune réponse exacte 



Poids apparent.
On dispose d'un ressort de masse négligeable, de constante de raideur  k = 5,4 N / m et de longueur à vide L₀ = 12 cm. L'extrémité supérieure est fixée à un support horizontal.
On suspend à l'extrémité inférieure de ce ressort une sphère métallique de rayon R = 1,5 cm. La longueur du ressort à l'équilibre est L₁ = 17 cm.
On immerge ensuite complètement  la sphère dans un liquide de densité d inconnue. La longueur du ressort à l'équilibre est L₂ = 15 cm.

Question : 

Calculer la densité du liquide.
 
0,62 ;

0,78 ;

0,85 ;
0,92 ;
0,98 ; 
aucune réponse exacte


Satellite.
Un satelitte de masse m= 530 kg décrit une trajectoire circulaire autour d'une planète de masse M.
Ce satellite se situe à une altitude de h =340 km par rapport à la surface de la planète.
La période de révolution du satellite est T = 1 h 34 min et sa vitesse vaut 7,13 km/s dans le référentiel planètocentrique.

Question : 

Parmi les affirmations suivantes, relatives à ce satellite, combien y en a t-il d'exactes ?
 
- Le rayon de la planète vaut R = 6,1 10³ km.
- la masse de la planète vaut M = 4,9 10²⁴ kg.
- la densité moyenne de la planète vaut d = 5,2.
- La force gravitationnelle exercée par la planète sur le satelitte a pour valeur F = 4,2 10³ N.
- Le satellite est soumis  à une accélération normale a_N =7,9 m s^-2.



Associations de résistors

Question : 

Déterminer U_BM en volt. 
2,0 ;
4,0 ;
6,0 ;
8,0 ;
16,0 ;
aucune réponse exacte



Solénoïde
On considère un solénoïde de longueur L = 60 cm dont l'axe est perpendiculaire à la direction de la composante horizontale B_H du champ magnétique terrestre. Une boussole est placée au centre du solénoïde.
Quand on fait circuler  un courant d'intensité constante I = 88 mA dans un sens donné, la direction de l'aiguille de la boussole fait un angle aigu a avec l'axe du solénoïde.
En inversant le sens du courant, l'aiguille de la boussole tourne de 151° par rapport à sa position précédente.

Question : 

Calculer le nombre de spires N de ce solénoïde.  
420 ;
450 ;
500 ;
520 ;
550 ;
aucune réponse exacte






La loupe
Un oeil normal voit tous les objets situés entre l'infini e la distance minimale de vision distincte D_m = 25 cm.
On utilise une loupe assimilée à une lentille mince convergente de vergence C = 6,0 dioptries.
Un observateur place son oeil " normal " au foyer image de la loupe.
Il regarde un objet AB, perpendiculaire  à l'axe principal de la loupe, le point A étant situé sur l'axe.
On note L la distance algébrisée entre le centre optique et A.
On notera L₁ la valeur que l'on doit donner  à L pour que l'image A' de A soit à l'infini.
On notera L₂ la valeur que l'on doit donner  à L pour que l'image A' de A soit située  à la distance minimale de vision distincte.
La latitude de mise au point de la loupe est L₂-L₁.

Question : 

Calculer la latitude de mise au point en cm. 

11 ;

14 ;

18 ;

20 ;

22 ;

aucune réponse exacte 

correction fixe
correction chimix

---

Radioactivité, pendule et projectile : concours kiné Berck 2010

Césium 137.
Le césium 137 subit une désintégration ß^- et le noyau fils est le baryum 137. 
Une source radioactive contient une masse m₀ =253 µg de césium 137 à la date t=0. 
On mesure l'activité de cette source à une date t₁ et on obtient la valeur A₁ = 5,67 10⁸ Bq.
On donne N_A = 6,02 10²³ mol^-1 ; 
masse molaire du césium 137 : M = 137 g/mol ; 
demi-vie du césium 137 : t_½ =30,17 années.

Question : Calculer la date t₁ en années. 
15,5 ;
17,8 ;
22,4 ;
25,6 ;
30,2 ;
aucune réponse exacte 





Fission de l'uranium 235
Dans un réacteur nucléaire, l'énergie est produite par la fission de l'uranium 235 sous le choc d'un neutron lent. Le combustible nucléaire utilisé est l'uranium naturel enrichi à 3,4 % en uranium 235 fissile.
Chaque fission d'un noyau d'uranium 235 libère en moyenne une énergie de 200 MeV.
Le rendement de la transformation de l'énergie nucléaire en énergie électrique est de 31 %.
Le réacteur consomme une masse m = 95,9 kg de combustible nucléaire en une journée.
On supposera que tous les noyaux d'uranium 235, contenus dans le combustible, subissent une fission.
On donne : 
masse molaire de l'uranium 235 : M = 235 g/mol ; 1 eV = 1,602 10^-19 J.
Question : Calculer la puissance électrique ( en GW) fournie par ce réacteur.
0,90 ;
0,92 ;
0,94 ;
0,96 ;
0,98 ; 
aucune réponse exacte 




Spectre d'émission
Le spectre d'émission de l'atome de sodium révèle la présence d'un doublet de raies jaunes de longueur d'onde l₁ =589,0 nm et l₂ = 589,6 nm.
Ces deux raies correspondent à une désexcitation de l'atome de sodium, à partir de deux niveaux d'énergie très proches, vers l'état fondamental.
Question : Déterminer l'écart d'énergie ( en meV ) entre ces deux niveaux.
1,2 ;
1,6 ;
2,1 ;
2,4 ;
2,5 ;
aucune réponse exacte


Balise.
Deux bateaux A et C sont séparés l'un de l'autre par une distance de 27 km et ils se trouvent dans le plan vertical contenant la balise.
Le bateau A capte le signal 7,7 s après son émission.
Le bateau C capte le signal de la balise 10,9 s après son émission.
Le son se propage à vitesse constante dans l'eau de mer  : v = 1,5 10³ m/s.
Question : Déterminer la profondeur h ( en km) à laquelle se trouve la balise.
2,3 ;
2,6 ;
2,9 ;
3,2 ;
3,5 ;
aucune réponse exacte

Pendule et projectile.
Masse de la spère : m = 250 g. On lâche la bille en A sans vitesse initiale. 
Quand la bille arrive en B, un dispositif spécifique la décroche du fil et elle continue son mouvement sous la seule action de son poids.
On note S le sommet de la trajectoire de la bille après son décrochage. 
On note P le point de contact avec le sol. 
On néglige l'action de l'air sur la bille dans toutes les phases du mouvement.
Coordonnées des points B et C : x_B =12,2 cm ; y_B =13,4 cm ; x_C =0 cm ; y_C =50,0 cm

Questions : 
Calculer la longueur L du fil constituant le pendule.
Calculer la vitesse en B, notée v_B ( m/s).

Calculer la tension T du fil en B.

Calculer l'ordonnée du sommet SCalculer l'abscisse du point P (en cm).


correction fixe
correction chimix

---

RLC Berck 2010

On réalise le circuit ci-dessus, composé :





- d'un condensateur de capacité C =2,00 µF ;

- d'une bobine d'inductance L = 250 mH et de résistance négligeable ;

- d'un conducteur ohmique de résistance R variable ;

 - d'un générateur idéal de tension de fem E = 25,0 V

- d'un interrupteur K à deux positions ;

- d'un capteur voltmètre relié à un ordinateur.

Etape n°1 : l'interrupteur K est en position 1 pendant le temps nécessaire pour que le condensateur se charge complètement.

Etape n°2 : on bascule l'interupteur K en position 2. Le circuit est le siège d'oscillations libres amorties.

Le capteur voltmètre permet d'enregistrer les variations de la tension u_C aux bornes du condensateur en fonction du temps.

On notera T la pseudo-période des oscillations électriques amorties.

Onadmettra que la résistance R est suffisamment faible pour que l'onpuisse confondre la pseudo-période T et la période propre T₀ des oscillations du circuit LC correspondant.

A la date t=T, la tension aux bornes du condensateur vaut u_C(T) = 19,7 V.

 
Quelques formules permettant de caractériser un régime pseudo-périodique  :

On montre que pour des dates t =kT ( avec k entier ):
la tension u_C se calcule par la relation : u_C(kT) = E exp(-kRT / (2L))
On définit le décrément logarithmique par la relation  : d = ln u_C(kT) / ln u_C((k+1)T)
Le facteur de qualité d'un régime pseudo-périodique se calcule par la relation : Q  = 2pi / d.

Questions :  
-Calculer la valeur de la pseudo-période T ( en ms).

-Déterminer la résistance R du conducteur ohmique.

-Calculer l'énergie perdue par effet Joule ( en µJ) au bout des 5 premières périodes.

-Calculer le facteur de qualité Q₀ ( sans unité ) du circuit.

-Quelle doit être la valeur de R ( en ohms)?

correction Chimix 
correction fixe

Pile argent aluminium ( Kiné Berck 2009)

Dans les deux solutions préparées la dissolution des solides est totale.
Solution 1 notée S₁ :
On prépare une solution de nitrate d'argent en dissolvant 10,2 g de nitrate d'argent solide AgNO₃ dans de l'eau distillée afin d'obtenir 500 mL de solution.
Solution 2 notée S₂ :
On prépare une solution de sulfate d'aluminium en dissolvant 10,4 g de solide Al₂(SO₄)₃, 18 H₂O dans de l'eau distillée pour obtenir 250 mL de solution.
Ag : 108; N : 14 ; O : 16 ; Al : 27 ; S : 32 ; H : 1 g/mol.
Réalisation de la pile :
On verse V₁ = 100 mL de solution S₁ dans le becher n°1 et on y plonge un fil d'argent.
On verse V₂ = 100 mL de solution S₂ dans le becher n°2 et on y plonge un fil d'aluminium.
Les deux demi-piles sont reliées par un pont salin contenant une solution saturée de nitrate d'ammonium.
Le circuit électrique extérieur est composé d'un ampèremètre, d'un conducteur ohmique de résistance R.
La pile fonctionne pendant une durée Dt et l'intensité constante du courant délivré est I = -22,1 mA


Au bout de la durée Dt on prélève V= 20,0 mL de la solution S₁. 
On remplit une burette graduée de chlorure de sodium de concentration apportée c'=1,00 10^-1 mol/L. La réaction du dosage est : Ag⁺aq + Cl^-aq = AgCl(s).
On plonge la sonde du conductimètre dans l'erlenmeyer. 
On verse la solution de chlorure de sodium, millilitre par millilitre et on mesure la conductivité s de la solution après chaque ajout.
Par détermination graphique on trouve qu'il faut verser V_éq =14,1 mL de solution de chlorure de sodium pour obtenir l'équivalence.
Données : 1F = 9,65 10⁴ C

 

Questions : 

Calculer la concentration effective initiale ( mol/L) des ions argent dans la solution S₁.

Calculer la concentration effective initiale ( mol/L) des ions aluminium dans la solution S₂.

Déterminer la durée Dt ( en min) de fonctionnement de la pile.  

Calculer la variation de masse Dm ( en mg) de l'électrode d'argent au bout de la durée Dt

Calculer la concentration effective finale ( mol/L) des ions aluminium dans la solution S₂.

correction chimix
correction fixe

---