Electricité générateur récepteurs resistances energie puissance 1ère S au concours

NANCY 2000
Correction des exos suivants : 

---

Deux piles Leclanché équivalentes alimentent respectivement les circuits A et B suivants:

Vrai ou faux?
1.la pile du circuit (A) a une durée de vie plus longue

2.les piles ont une durée de vie identique
3.la pile du circuit (B) a une durée de vie plus longue

---

Une automobile laisse fonctionner 2 phares (puissance 45 W chacun) et 4 feux de position (puissance individuelle 15 W). 
Le moteur est arrêté. 
La batterie de résistance interne négligeable a une capacité de 40 Ah et une fem de 12 V
Vrai ou faux?
1.Les 6 ampoules sont montées en série
2.Les 2 phares sont en série et les 4 feux de positions de même. Ces 2 associations sont branchées en dérivation l'une par rapport à l'autre.
3.Les 6 ampoules sont montées en parallèle.

---

Quelques unités :

Vrai ou faux?
1.    L'unité de puissance est le joule
2.    2 MV signifie 2 millivolts
3.    dans l'expression C=10 µF , F désigne le faraday
4.    une charge électrique se mesure en coulomb

---

G générateur 12V et 2 ohms
G' générateur 50V et 5 ohms
R=10 ohms conducteur ohmique
E électrolyseur 2V; 3 ohms


Vrai ou faux?Le courant I vaut (A) :

°3,1
°3
°1,8
°2

---

Paris 2000
correction des exos suivants

---

Un générateur de tension continue a une f e m de 30 V et une résistance interne r= 6 ohms.
Il fournit une puissance de 31,5 W à un circuit extérieur résistif.
Vrai ou faux?L'intensité dans le circuit est :

°   2 A
°   3 A
°   3,5 A
°   1,5 A
°   1 A

EFOM 2001 correction fixe Une génératrice G de f.é.m. E = 62 V et de résistance interne r = 2 ohm,alimente un moteur électrique M, de f.c.é.m. E' = 48 V et de résistance interne r' = 20 ohm. La ligne est composée de deux fils de cuivre PA et NB. Chacun de ces fils possède une résistance R = 5 ohm. question : Déterminer l'intensité I du courant débité par la génératrice.   question : Déterminer les tensions U et U' aux bornes du générateur et du moteur.  En déduire la chute de tension le long de cette ligne: U - U'.   Le courant passe pendant un intervalle de temps Δt = 100 s. question : Déterminer : - l'énergie électrique Wél fournie par la génératrice au reste du circuit - l'énergie électrique W'él reçue par le moteur de la part du reste du circuit  - la chaleur dégagée par la ligne, qui est en régime permanent : - le rendement h de la ligne. Le rendement dépend-il de la durée du passage du courant ? Données : 4,8/6,2 = 0,774 ; 5/6 = 0,833 La génératrice est actionnée par une turbine, le moteur fait tourner l'arbre d'une machine-outil. question : Déterminer le travail fourni par la turbine à la génératrice, pendant 100 s. question : Déterminer le travail fourni par le moteur à la machine-outil, pendant 100 s. Les appareils sont en régime permanent, l'effet Joule représente pratiquement la seule source de chaleur. question : Définir et déterminer le rendement de l'installation: génératrice, ligne, moteur. Berck 2001 Le moteur d'une grue soulève une charge de 30 000 N à la vitesse de 15 m/min. La tension d'alimentation continue du moteur est U=230V et l'intensité du courant vaut i=45 A. Le rapport de la puissance mécanique fournie à la puissance électrique utile du moteur (rendement mécanique) est de 75%. question :Quelle est la résistance r du moteur (en ohm) ? (remarque : l'énergie mécanique est le produit scalaire F (vecteur).distance (vecteur) et la puissance mécanique est énergie/temps.) °  0,96 °  0,42 °  0,17 °  0,64 °  0,23 °  0,85 élément de réponse :  correction des exos suivants : Ascq 2002 Parmi les propositions suivantes concernant certains dipôles électriques lesquelles sont vraies ? 1)Quand on branche un voltmètre aux bornes d'une pile à vide on mesure la force électromotrice de la pile 2)Un conducteur ohmique transforme l'intégralité de l'énergie électrique qu'il reçoit en énergie calorifique. 3)La caractéristique u = f(i) d'un résistor est une fonction linéaire croissante. Le générateur (E= 5,5 V et r = 2,25 ohms) est  branché aux bornes d'un conducteur ohmique de résistance R= 12 ohms. On se propose de déterminer l'énergie calorifique dégagée dans le conducteur ohmique pendant une durée de 15 min. l'énergie dégagée dans le conducteur ohmique a pour valeur ( en kJ) aide : i (A) = E / ( R+r) U= R i énergie (J) = U i t le temps est en seconde réponses possibles : 9,22 0,15 2,81 1,61 8,52 4,61 14,12 6,21 Un générateur de force électromotrice E et de résistance interne r alimente successivement deux circuits différents et fournit : - dans le circuit n°1 : une puissance P1=1,84 W quand la tension entre ses bornes vaut U1=4,6 V - dans le circuit n°2 : une puissance P2 =2,96 W quand la tension entre ses bornes vaut U2=3,7 V Question : La force électromotrice E du générateur a pour valeur ( en volt) : aide : puissance (watt) = tension (volt) fois intensité (ampère) I 1 = 1,84 / 4,6 = 0,4 A I 2 = 2,96 / 3,7 = 0,8 A puis U= E-r I, tension aux bornes de la pile 4,6 = E-0,4 rI 3,7 = E -0,8 r réponses possibles : 10,2 7,8 6 4,9 6,9 9,5 5,5 8,9  Un générateur de force électromotrice E et de résistance interne r alimente successivement deux circuits différents et fournit : - dans le circuit n°1 : une puissance P1=1,84 W quand la tension entre ses bornes vaut U1=4,6 V - dans le circuit n°2 : une puissance P2 =2,96 W quand la tension entre ses bornes vaut U2=3,7 V La résistance interne du générateur a pour valeur ( en ohm) : aide : puissance (watt) = tension (volt) fois intensité (ampère) I 1 = 1,84 / 4,6 = 0,4 A I 2 = 2,96 / 3,7 = 0,8 A puis U= E-r I, tension aux bornes de la pile 4,6 = E-0,4 rI 3,7 = E -0,8 r Réponses possibles : 1,25 3,25 4,2 2,8 4,9 4,8 3,75 2,25  Nantes 2003 R1 = 60 W ; R2 = 40 W ; R3 = 30 W ; E=9 V ; r=6 W. Calculer les intensités I, I1, I2. correction fixe ( à la suite d'un autre exo) Nantes 2004 E= 12 V ; R1 est la résistance d'un photorésistor ( conducteur dont la résistance varie avec l'éclairement) ; R2= 20 kW ; R3= 18 kW ; R4= 24 kW ; Questions :  Exprimer la tension UAN en fonction de E, R1 et R2. Exprimer la tension UBN en fonction de E, R3 et R4. Exprimer la tension UAB en fonction de E, R1, R2, R3 et R4. - Etablir la condition sur R1, R2, R3 et R4 pour que UAB=0 - Calculer R1 si UAB=0. Un voltmètre indique UAB= 100 mV. Calculer R1 correction fixe ( à la suite d'un autre exo)  Rennes 2005 : association de resistors Pour chaque réponse donner l'expression littérale, puis la valeur de la grandeur recherchée. On prend R= 10 W , R1=2R et R2 = 3 R. - Quelle est la résistance équivalente au circuit ? - Déterminer l'intensité du courant i. - Déterminer les tensions UAB et UDC. Dans cette partie R= R1=R2. - Quelle doit être la valeur de R pour que l'intensité du courant soit i= 0,40 A ? - Quelle est alors l'énergie dissipée par effet joule par R en 1 min ? - Quelle est l'énergie fournie au circuit par le générateur pendant ce même laps de temps ? - On ouvre l'interrupteur K, déterminer les tensions UAB et UDC. 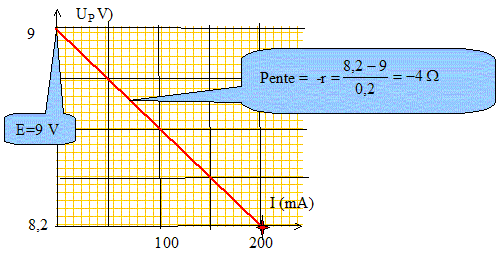correction fixe ( à la suite d'un autre exo)  CEERRF 2006  On dispose du matériel suivant : une pile "9 V", cinq conducteurs ohmiques de résistances R= 20 W, deux multimètres, des fils, un jouet ( petite grue doté d'un moteur électrique), une notice du moteur de la grue sur laquelle on peut lire " puissance électrique maximale tolérée = Pmax = 3 W". Tension aux bornes du moteur électrique U= E'+ r' I avec E' : force électromotrice du motuer et r': résistance électrique du moteur Etude de la pile : on réalise un montage qui permet de tracer la caractèristique intensité-tension de la pile, c'est à dire la courbe représentant l'évolution de la tension UPN aux bornes de la pile en fonction de l'intensité I qu'elle débite. Déterminer les valeurs de la fem E et de la résistance interne r de la pile. On relie brievement les deux bornes de la pile par un fil de jonction ( de résistance nulle). Quelle est la valeur de la tension aux bornes de la pile ? Quelle est la valeur de l'intensité délivrée par la pile ? On défait le montage précédent et on monte en série la pile et deux conducteurs ohmiques de résistance R. Quelle est l'intensité du courant à travers ce circuit ? Etude du moteur de la grue : on décide de faire fonctionner le moteur grâce à la pile de 9 V. Dans un premier temps, on envisage de relier directement la pile aux bornes du moteur. L'intensité du courant dans ce circuit est alors I= 0,75 A. Le moteur est-il endommagé ? Justifier. Dans un deuxième temps, on envisage de de monter en série, la pile, un résistor de résistance R'= 5 W et le moteur. Comment peut-on réaliser un dipôle ohmique de résistance R' = 5 W ? - Faire le schéma du circuit électrique réalisé. Utilisation de la grue : une charge de masse m= 1 kg est posée au sol, à côté de la grue ; le fil indéformable est tendu. On fait tourner le moteur électrique pendant t= 5,0 s, ce qui a pour effet d'enrouler le fil sur l'arbre du moteur et ainsi de lever la charge d'une hauteur totale h= 75 cm. On considère que le mouvement de la charge est rectiligne et uniforme pendant la montée. L'intensité du courant dans le circuit vaut I= 0,5 A. g = 10 m/s². Quelle est la tension aux bornes de la pile durant la montée de la charge ? - Calculer l'énergie électrique fournie par la pile en 5 s. - Calculer l'énergie totale engendrée par la pile en 5 s, c'est à dire la diminution d'énergie chimique contenue dans la pile. On admet que les deux seules forces qui s'exercent sur la charge sont son poids et la force exercée par le fil ; On suppose que le travail mécanique fourni par le moteur est égal au travail de la force exercée par le fil sur la charge. - Etablir l'expression de la puissance mécanique Pm que développe le moteur durant la montée en fonction de h et de m. - Quelle est l'expression de la fcem E' du moteur en fonction de Pm ? On donne 9/24 = 0,375 ; 9/44 = 0,2045. correction fixe ( à la suite d'un autre exo) Berck 2007 UAD=7,5 V Calculer UBC (V).  Réponses possibles :  1,0 ;  2,5 ;  3,5 ;  4,5 ;  7,5;  aucune réponse exacte correction fixe ( à la suite d'un autre exo)

St Michel 2007
Un générateur de courant continu de fem E=6,0 V et de résistance interne r=2,0 ohms est connecté à un circuit extérieur de telle sorte qu'il fournisse la puissance maximale dont il est capable. 
question : Le rendement du générateur est égal ( en %) à :  
40 ; 
50 ; 
60 ; 
70 ; 
90.
question : Dans les conditions précédentes, le générateur dissipe par effet joule une puissance (W) égale à :
3 ; 
3,5 ;
4 ; 
4,5 ;
5.
correction fixe ( à la suite d'un autre exo)

---

CEERRF 2008
correction fixe ( à la suite d'un autre exo)
On considère deux conducteurs ohmiques identiques ( résistance R), et un générateur de tension ( E=30 V, r₁= 10 Ω).
Pour mesurer la tension à vide ( f.e.m) de ce générateur on branche un voltmètre à ses bornes.
question : 
Expliquer à l'aide d'un calcul, pourquoi on mesure bien la tension à vide ( f.e.m ), la résistance du voltmètre notée R_V étant très grande.

On associe les deux conducteurs ohmiques en parallèle et on les relie au générateur.
Un ampèremètre branché dans le circuit mesure une intensité I=500 mA.
question : Exprimer I en fonction des données.
question :En déduire l'expression littérale et la valeur de R.

---

Assas 2008 : 
correction fixe ( à la suite d'un autre exo)Il est demandé l'expression des valeurs littérales avant tout calcul numérique. Les notations du texte doivent être respectées.
Le circuit élctrique d'une petite grue en jouet est constitué d'un circuit série comprenant :
une pile électrique dont la caractéristique U_P(I) est donnée ci-dessous,
un résistor de résistance variable R
et un moteur de f.c.e.m E' = 3,0 V et de rendement r_M=0,6.
L'énegie mécanique délivrée par le moteur sert à faire monter et descendre verticalement une petite masse
m =30 g d'une hauteur h = 1,0 m à la vitesse constante v = 0,50 m/s.
On constate que la pile est épuisée lorsque la masse a effectué 50 montées et descentes. g= 10 m/s².

Question : Calculer la puissance mécanique P_M délivrée par le moteur, la puissance électrique P _elM qu'il consomme et l'intensité I du courant qui le traverse.

Question : Déterminer la f.e.m E et la résistance interne r de la pile, la puissance chimique P_ch mise en jeu, la puissance P_elP qu'elle fournit au circuit.

Question : Calculer l'énergie chimique totale délivrée par la pile ainsi que l'énergie dissipée dans le résistor de résistance R.

---

Q.C.M. 2007
correction fixe ( à la suite d'un autre exo)

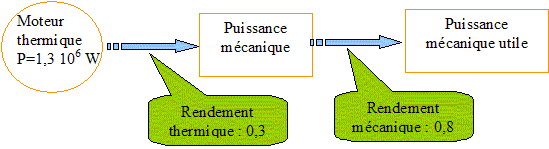
Question : Quelle la puissance mécanique utile ?

Puissance et énergie.
L' énergie mise en oeuvre W= 3 10⁶ J pendant une durée Δt = 8 heures.
Question :Quelle est la puissance moyenne correspondante ?

Energie est en Joule.
Question :Quelles sont les autres unités de l'énergie ?

---

Moteur
Texte:

moteur bloqué I = 5A
fonctionnement normal I=2,5 A

Question : Quelle est la résistance interne du moteur?
Question : Quelle est  la fcem E' du moteur ?
Question : Quelle est la puissance P_elect des forces électromagnétiques?

Moteur

E = 12 V ; r = 2 W ; E' = 9 V ; r' = 3  Ω.
Question : Quelle est  l'intensité I?
Question :Quelle est la tension U aux bornes du moteur?
Question :Quelles sont les puissances mises en jeu?.
correction fixe ( à la suite d'un autre exo)

---

Ceerrf 2009
correction fixe ( à la suite d'un autre exo)

On considère un générateur caractérisé par sa tension à vide E1 et sa résistance interne r1.
En circuit fermé il débite un courant d'intensité I.

Question : Rappeler la loi d'Ohm pour ce générateur et faire un schéma équivalent d'un tel générateur.

Question :

Rappeler les expressions de la puissance totale P_G échangée par ce générateur, de la puissance P_e échangée avec le circuit extérieur, de la puissance P_J dissipée par effet Joule dans le générateur.

Question :
En déduire l'expression deW_J , W_{G ,}W_{e ,} E₁, r₁, rendement h. et les calculer :

On associe ce générateur en parallèle avec un autre générateur de tension à vide E₂ = E₁ et de résistance interne r₂ inconnue, de telle sorte que les bornes positives coïncident.
 Question :

Schématiser l'association.

 (Partie de Réponse :

On note I₁ l'intensité débitée par le premier générateur et I₂ l'intensité débitée par le second.

 fin de réponse)

On considère que cette association est équivalente à un seul générateur de caractéristique E_éq et r_éq, de tension U_PN et débitant un courant d'intensité I.
Question :

Etablir les expressions littérales de I₁, I₂ en fonction de r₁, r₂ et I.

En déduire l'expression de E_éq puis celle de r_éq.

Question :

Donner l'expression des puissances électriques P₁, P₂ et P_éq disponibles aux bornes de chaque générateur puis aux bornes du générateur équivalent.

Question :

Calculer r₂ si r_éq = 5,0 ohms.

---

EFOM 2009
correction
Moteur électrique.
Un moteur électrique ( fcem E' = 1,25 V, r' = 1 ohm) est associé en série avec un générateur ( fem E = 4,5 V, r = 1,5 ohms) et un conducteur ohmique R = 4 ohms.
Intensité du courant dans le circuit?

A °0,5 A
B °1 A
C °0,05 A
D ° 0,1 A
E °1,2 A
F °autres

Calculer pour 3 min de fonctionnement, l'énergie totale fournie par la pile.

A °125 J
B °250 J
C °12,5 J
D °405 J
E °35 J
F °autre

Calculer pour 3 min de fonctionnement, l'énergie consommée dans le conducteur ohmique.

A °125 J
B °250 J
C °215 J
D °405 J
E °35 J
F °autre

Calculer pour 3 min de fonctionnement, l'énergie utile produite par le moteur.

A °125 J
B °250 J
C °12,5 J
D °405 J
E °112,5 J
F °autre

---

Berck 2009
Moteur électrique.
Un moteur est branché à une pile de fem E = 6,0 V et de résistance interne r = 1,2 ohms.
Le générateur fourni une puissance électrique de 2,8 W au moteur qui en convertit 80 % en énergie mécanique.
Déterminer la résistance électrique ( ohms) du moteur : 

Réponses possibles

2,1
4,2
6,7
8,2
9,8
autre

---

 CERRFF 2010
Dipole électrique linéaire.
La caractéristique intensité tensiond'un dipole électrique linéaire passe par les deux points de fonctionnement A ( 300 mA ; 14 V) et B ( 1,5 A ; 2,0 V).
On peut affirmer que :
A- ce dipole est à classer dans la catégorie des récepteurs. 
B- La loi de fonctionnement de ce dipole est de la forme I = a U + b avec a< 0 et b >0.
C- Lorsqu'il fonctionne au maximum de sa puissance ce dipole délivre une intensité de 850  mA. 
D- Si U = 10 V alors I = 1,0 A.
E- Ce dipole dissipe par effet joule, une puissance du type rI²t.

---

EFOM 2010

Associations de conducteurs ohmiques.

U_AD = 15 V ; R = 16 ohms.
A- La tension U_BC vaut environ 5,0 V.  
B-  La résistance équivalente du circuit vaut environ 30 ohms. 
C- Les tensions U_BC et U_CD sont identiques.
D- L'intensité vaut environ 0,50A.
F- Aucune de ces propositions n'est exacte.

---

Berck 2010
Associations de résistors.

Déterminer U_BM en volt. 
2,0 ;
4,0 ;
6,0 ;
8,0 ;
16,0 ;
aucune réponse exacte

---

Oscillateur mécanique, ondes sur une corde, chute dans un fluide, photon AP HP 2009

Répondre par Vrai ou faux :  
Pendule simple.
Un pendule simple de masse m = 10 g, de longueur L = 1 m est écarté de sa position d'équilibre d'un angle égal à 8 °.
On le lâche sans vitesse initiale et on néglige les frottements.
Le plan horizontal contenant la position d'équilibre, est choisi comme référence de l'énergie potentielle.
On donne cos 8° = 0,99 et g ~ 10 m s^-2.

Analyse : période du pendule.
A-la période du pendule est inversement proportionnelle à la racine carrée de sa masse.

Analyse : vitesse maximale.
B- v_max = (2E_m/m)^½ avec E_m, énergie mécanique du pendule.  

Analyse : valeur de l'énergie mécanique.
C- E_m = 1 mJ.  

D- la vitesse de la masse est égale à la moitié de sa vitesse maximale quand l'énergie cinétique est égale au quart de son énergie mécanique.  

---

Ondes mécaniques.
On attache une corde AB de longueur L = 4,0 m à l'extrémité d'un vibreur.
Ce vibreur produit le long de la corde une déformation sinusoïdale de fréquence f = 100 Hz.
La corde est maintenue horizontale.
l'autre extrémité passe dans une poulie sans frottements.
A l'extrémité libre du fil on attache une masse m = 200 g. Ainsi la tension de la corde est égale au poids de la masse. Un système permet d'éviter les réflexions des ondes sur l'extrémité libre.
La célérité le long de la corde est v = (T/µ)^½ où T est la tension de la corde et µ la masse linéique de la corde.
On donne µ = 20 g cm^-1

Analyse : tension de la corde. A-la tension de la corde s'exprime en kg m s^-1.  

Analyse : célérité de l'onde.
B- la célérité de l'onde augmente avec la masse linéique de la corde.

Analyse : amortissement.
C-la corde est le siège d'oscillations amorties.  

Analyse : longueur d'onde.
D- la longueur d'onde est l = 10 cm.  

---

Chute dans un fluide : Les vecteurs sont écrits en gras et en bleu.
On considère trois billes sphériques homogènes de rayon identique, de même volume V_B faites de trois matières différentes avec les masses volumiques respectives : r₁ =900 kg m^-3 ; r₂ =110 kg m^-3 ; r₃ =1300 kg m^-3. les trois billes sont lâchées sans vitesse initiale dans un fluide de masse volumique r =1000 kg m^-3 de la même altitude correspondant à la surface libre du fluide.
Les billes en mouvement dans le fluide sont soumises à une force de frottement f = -k v avec k coefficient identique pour les trois billes et v : vitesse du centre de la bille.

Analyse : équation différentielle.
A-le mouvement de la bille 1 est régi par l'équation différentielle : dv/dt + k / (r₁V_B) v =(1 -r / r₁) g.  

Analyse : poussée d'Archimède.
B- la poussée d'Archimède exercée sur la bille 1 est plus intense que la poussée exercée sur la bille 3.  

Analyse : quelle bille flotte ?
C-aucune bille ne flotte.  

Analyse : vitesse limite.
D- la bille 3 admet une vitesse limite supérieure à celle de la bille 2.  

---

A propos d'une molécule : La liaison chimique entre deux atomes d'une molécule peut être modélisée par un ressort de constante de raideur k. La période propre de ce système est la même que celle d'un oscillateur élastique de constante de raideur k et de masse égale à la masse réduite µ = m₁ m₂ /(m₁+m₂), m₁ et m₂ représentant les masses des deux atomes constituant la molécule.
On donne : µ = 1,58 10^-27 kg ;
c = 3 10⁸ m/s ;
pi²~ 10 ;
1,2²*1,58 = 2,3 ;
1,2²/1,58 = 0,9 ;
1,58 / 1,2² = 1,09 ;
1,2*1,58² = 3 ;
1,2 / 1,58² = 0,5.
Ce système peut entrer en résonance lorsqu'il est excité par des ondes électromagnétiques.
Des mesures permettent de montrer que la molécule de fluorure d'hydrogène absorbe des ondes de longueur d'onde dans le vide de 2,5 µm.

Analyse : domaine de l'onde absorbée.
A-la molécule de fluorure d'hydrogène absorbe dans l'ultra-violet.  

Analyse : fréquence de l'onde.
B- la valeur de la fréquence de la radiation absorbée par la molécule est 1,2 10⁶ Hz.  

Analyse : fréquence propre.
C-la fréquence propre de l'oscillateur a pour expression f = 2 pi(µ/k)^½.  

Analyse : coefficient de raideur k.
D- k = 920 N m^-1.  


<sup>correction fixe 

correction chimix</sup>

---

Energie : saut à l'élastique, énergie nucléaire ( plutonium), énergie électrique ( dipôle LC) AP HP 2009

Saut à l'élastique.
Les vecteurs sont écrits en gras et en bleu.
Lors d'un saut à l'élastique, un candidats aux frissons, de masse m, s'élance d'un pont situé à une hauteur h au dessus du sol.
L'élastique de masse négligeable se comporte comme un ressort de longueur à vide l₀ = 0,25 h et de constante de raideur k.
Une des extrémités de l'élastique est accrochée au pont et l'autre extrémité est accrochée au sauteur.
On admettra que le mouvement s'effectue selon la verticale et on suppose que les frottements sont négligeables.
On considère un axe verticale Oy orienté vers le haut et dont l'origine est située au niveau du sol.
On notera u le vecteur unitaire lié à l'axe Oy et g l'intensité de la pesanteur.
La position du sauteur assimilé à son centre d'inertie est repérée par sa distance au sol y.
On posera l'énergie potentielle de pesanteur nulle au sol et l'énergie potentielle élastique nulle pour l'élastique à vide.

Question : Faire le bilan des forces subies par le sauteur.

Question : Etablir l'expression donnant la résultante des forces en fonction de m, k, g, y et u , lorsque le sauteur est à une altitude comprise entre y = 0 et y = 0,75 h.
Question : Donner l'expression de l'énergie potentielle élastique E_{p élas} pour une altitude y comprise entre y = 0 et y = 0,75 h.
Question : En déduire l'expression donnant l'énergie potentielle du système à cette même altitude.
Question : En supposant que la vitesse initiale du sauteur soit nulle, au delà de quelle valeur de la constante de raideur k, le saut est-il sans danger, c'est à dire que le sauteur touche le sol avec une vitesse nulle ?

Energie nucléaire.
Certains appareils utilisés en médecine utilisent du plutonium ²³⁸₉₄Pu qui se désintègre en émettant une particule alpha d'énergie cinétique Ec(a) = 12 MeV.
La demi-vie du plutonium 238 est t_½ = 5,6 10⁹ s.
La source contenant une masse m = 29,75 mg de plutonium 238 est scellée hermétiquement dans un récipient, l'énergie étant alors transformée en énergie thermique.
On donne : N_A = 6,0 10²³ mol^-1 ; c = 3,0 10⁸ m/s ; h = 6,4 10^-34 J s ; ln 2 = 0,70 ; ln5 = 1,6 ; ln7,= 2,0 ; 1 MeV = 1,6 10^-13 J.
 Question : Quelles sont les grandeurs physiques conservées lors de la désintégration du plutonium 238 ?

Question : Ecrire l'équation de désintégration du plutonium 238. Préciser le nombre de neutrons du noyau fils.

Question : Les énergies de liaison par nucléon sont notées E_l(Pu), E_l(a), E_l(^A_ZX).  
Etablir l'expression de l'énergie libérée lors de la désintégration en fonction des énergies de liaison par nucléon.

Question : Donner l'expression du nombre d'atomes de plutonium initialement présents dans la source utilisée. Faire l'application numérique.

Question : Donner l'expression de la puissance thermique initiale P_th0 puis calculer sa valeur.

Question : Exprimer puis calculer le rendement de la conversion.


Question : La pile fonctionne de façon correcte tant que sa perte de puissance reste inférieure à 30% de sa puissance initiale.
Exprimer puis calculer la durée pendant laquelle la source peut fonctionner de façon correcte.

Question : La désintégration du plutonium 238 s'accompagne d'émission de photons, chacun d'énergie E = 1,5 MeV.
Calculer la longueur d'onde des photons émis.


Energie électrique : On considère un circuit électrique formé d'un condensateur 
de capacité C =25 µF, d'une bobine d'inductance L = 40 mH, de résistance nulle 
et d'un interrupteur.
A l'instant t=0 on ferme l'interrupteur, le condensateur possédant alors une énergie de 50 µJ.
On prendra pi ~ 3.
Question : Comment nomme t-on ce type d'oscillateur ?

Question : Donner l'expression de la période et calculer sa valeur.


Question : Exprimer puis calculer la tension initiale U₀ aux bornes du condensateur.

Question : Etablir l'équation différentielle régissant l'évolution de la charge d'un armature du condensateur au cours du temps

Question : La solution de cette équation différentielle est de la forme q(t) = A cos (wt+f).
Donner les expression de A, w et f en justifiant.

Question : Etablir l'expression W_el(t) de l'énergie stockée dans le condensateur au cours du temps.


Question : Donner l'allure de la courbe donnant l'évolution de W_el(t) sur deux périodes

Question : Etablir l'expression W_mag(t) de l'énergie stockée dans la bobine au cours du temps.  

Question : Donner l'allure de la courbe donnant l'évolution de W_mag(t) sur deux périodes

Question : En réalité la bobine n'est pas idéale.
Par un bilan de puissance, établir l'équation différentielle régissant l'évolution de la charge au cours du temps.


correction fixe
correction chimix

Radioactivité, pendule et projectile : concours kiné Berck 2010

Césium 137.
Le césium 137 subit une désintégration ß^- et le noyau fils est le baryum 137. 
Une source radioactive contient une masse m₀ =253 µg de césium 137 à la date t=0. 
On mesure l'activité de cette source à une date t₁ et on obtient la valeur A₁ = 5,67 10⁸ Bq.
On donne N_A = 6,02 10²³ mol^-1 ; 
masse molaire du césium 137 : M = 137 g/mol ; 
demi-vie du césium 137 : t_½ =30,17 années.

Question : Calculer la date t₁ en années. 
15,5 ;
17,8 ;
22,4 ;
25,6 ;
30,2 ;
aucune réponse exacte 





Fission de l'uranium 235
Dans un réacteur nucléaire, l'énergie est produite par la fission de l'uranium 235 sous le choc d'un neutron lent. Le combustible nucléaire utilisé est l'uranium naturel enrichi à 3,4 % en uranium 235 fissile.
Chaque fission d'un noyau d'uranium 235 libère en moyenne une énergie de 200 MeV.
Le rendement de la transformation de l'énergie nucléaire en énergie électrique est de 31 %.
Le réacteur consomme une masse m = 95,9 kg de combustible nucléaire en une journée.
On supposera que tous les noyaux d'uranium 235, contenus dans le combustible, subissent une fission.
On donne : 
masse molaire de l'uranium 235 : M = 235 g/mol ; 1 eV = 1,602 10^-19 J.
Question : Calculer la puissance électrique ( en GW) fournie par ce réacteur.
0,90 ;
0,92 ;
0,94 ;
0,96 ;
0,98 ; 
aucune réponse exacte 




Spectre d'émission
Le spectre d'émission de l'atome de sodium révèle la présence d'un doublet de raies jaunes de longueur d'onde l₁ =589,0 nm et l₂ = 589,6 nm.
Ces deux raies correspondent à une désexcitation de l'atome de sodium, à partir de deux niveaux d'énergie très proches, vers l'état fondamental.
Question : Déterminer l'écart d'énergie ( en meV ) entre ces deux niveaux.
1,2 ;
1,6 ;
2,1 ;
2,4 ;
2,5 ;
aucune réponse exacte


Balise.
Deux bateaux A et C sont séparés l'un de l'autre par une distance de 27 km et ils se trouvent dans le plan vertical contenant la balise.
Le bateau A capte le signal 7,7 s après son émission.
Le bateau C capte le signal de la balise 10,9 s après son émission.
Le son se propage à vitesse constante dans l'eau de mer  : v = 1,5 10³ m/s.
Question : Déterminer la profondeur h ( en km) à laquelle se trouve la balise.
2,3 ;
2,6 ;
2,9 ;
3,2 ;
3,5 ;
aucune réponse exacte

Pendule et projectile.
Masse de la spère : m = 250 g. On lâche la bille en A sans vitesse initiale. 
Quand la bille arrive en B, un dispositif spécifique la décroche du fil et elle continue son mouvement sous la seule action de son poids.
On note S le sommet de la trajectoire de la bille après son décrochage. 
On note P le point de contact avec le sol. 
On néglige l'action de l'air sur la bille dans toutes les phases du mouvement.
Coordonnées des points B et C : x_B =12,2 cm ; y_B =13,4 cm ; x_C =0 cm ; y_C =50,0 cm

Questions : 
Calculer la longueur L du fil constituant le pendule.
Calculer la vitesse en B, notée v_B ( m/s).

Calculer la tension T du fil en B.

Calculer l'ordonnée du sommet SCalculer l'abscisse du point P (en cm).


correction fixe
correction chimix

---

Oscillateur électrique ( RLC) : Berck 2010

On réalise le circuit ci-dessus, composé :
- d'un condensateur de capacité C =2,00 µF ;
- d'une bobine d'inductance L = 250 mH et de résistance négligeable ;
- d'un conducteur ohmique de résistance R variable ;
- d'un générateur idéal de tension de fem E = 25,0 V
- d'un interrupteur K à deux positions ;
- d'un capteur voltmètre relié à un ordinateur.

Etape n°1 : l'interrupteur K est en position 1 pendant le temps nécessaire pour que le condensateur se charge complètement.

Etape n°2 : on bascule l'interrupteur K en position 2. Le circuit est le siège d'oscillations libres amorties.
Le capteur voltmètre permet d'enregistrer les variations de la tension u_C aux bornes du condensateur en fonction du temps.
On notera T la pseudo-période des oscillations électriques amorties.
On admettra que la résistance R est suffisamment faible pour que l'on puisse confondre la pseudo-période T et la période propre T₀ des oscillations du circuit LC correspondant.
A la date t=T, la tension aux bornes du condensateur vaut u_C(T) = 19,7 V






Quelques formules permettant de caractériser un régime pseudo-périodique :
°On montre que pour des dates t = kT ( avec k entier ), la tension u_C se calcule par la relation :
u_C(kT) = E exp(-kRT / (2L))
°On définit le décrément logarithmique par la relation  :  
d = ln u_C(kT) / ln u_C((k+1)T)
°Le facteur de qualité d'un régime pseudo-périodique se calcule par la relation :  
Q  = 2 pi / d. 

 Questions :

Calculer la valeur de la pseudo-période T ( en ms).

Déterminer la résistance R du conducteur ohmique.

Calculer l'énergie perdue par effet Joule ( en µJ) au bout des 5 premières périodes.

Calculer le facteur de qualité Q₀ ( sans unité ) du circuit.

Quelle doit être la valeur de R ( en ohms) ?


correction fixe
correction chimix

haute voltige, concours kiné AP-HP 2010

Au cirque lors d'un numéro de haute voltige, un trapéziste A s'élance à partir d'un trampoline situé au sol et est rattrapé par un autre trapéziste B situé en hauteur. Le but de ce problème est d'étudié la trajectoire du premier trapéziste assimilé à son centre d'inertie et de mettre en corrélation les mouvements des deux trapézistes pour que la figure soit réussie.

Les parties I, II et III peuvent être traitées indépendamment.

I. Etude du premier trapéziste.

Le trapéziste de masse mA est lancé d'un point O avec une vitesse initiale v₀, contenue dans le plan vertical Oxy et faisant un angle q avec l'axe horizontal Ox. 

Ce trapéziste est soumis à une force de frottement proportionnelle à la vitesse v :

Q : Etablir l'équation différentielle vérifiée par le vecteur vitesse caractérisant le mouvement.

Etude sur l'axe horizontal Ox.
Q : 

-Ecrire l'équation différentielle vérifiée par la composante v_x de la vitesse.

-En déduire à l'aide des conditions initiales la composante  v_x( t).

-En intégrant l'équation précédente, déduire l'équation horaire x(t).

Etude sur l'axe horizontal Oy

Q : Ecrire l'équation différentielle vérifiée par la composante v_y de la vitesse.

En déduire à l'aide des conditions initiales la composante  v_y( 0).

Que deviennent les composantes v_x et v_y de la vitesse lorsque t tend vers l'infini?

Montrer que lorsque t tend vers l'infini, la trajectoire admet une asymptote. Donner l'allure de la trajectoire de A

Donner l'allure de la trajectoire de A.

Q : Dans la question suivante, on néglige les frottements.
Quelles sont les équations horaires du mouvement de A ? En déduire l'équation de la trajectoire.

II. Trajectoire de B placé en réception.
Les frottements sont négligés.
Le trapéziste B assimilé à son centre d'inertie, de masse m_B se balance sur un trapèze assimilé à un pendule, constitué d'un fil inextensible de longueur L, de masse m_P.
On posera m = m_A + m_P.  On prendra l'état d'équilibre pour l'état de référence de l'énergie potentielle.
Le trapéziste s'élance sans vitesse initiale à la date t=0, d'une hauteur h au dessus du sol, le trapèze faisant un angle a₀ avec la verticale.
A une date quelconque t, la position du trapèze est repérée par l'angle a que fait le fil avec la verticale.

 
Q : 

 Etablir à la date t, en fonction de m, g, L et a :
- l'expression de l'énergie potentielle 

- expression de l'énergie cinétique.

- expression de l'énergie mécanique.

-Justifier que l'énergie mécanique se conserve.

-Equation différentielle vérifiée par a.

( on admettra que l'approximation des petits angles est valable sin a ~a)

La solution est supposée de la forme a(t) = A cos (Bt+C) avec A >0.
Q : A l'aide des conditions initiales et de l'équation différentielle, déterminer A, B et C.

Lorsque, au cours du mouvement le trapéziste se balance, il est soumis à une force T due au fil.
Q : Montrer que la valeur de T au point M de la trajectoire peut s'exprimée par la relation :
T = m( v²_E/ l + g ( 3 cos a-2)) où v_E est la vitesse au passage à la position d'équilibre.

II. La figure d'accrochage.
Les frottements sont négligés.
Le trapéziste A de masse 80 kg s'élance à la date t=0 de O à la vitesse de 20 m/s avec un angle  
q = 45 °. Le trapèze se trouve à la distance  d = 20 m du trapéziste A et à une hauteur de 10 m au dessus du sol. Le fil du trapèze a une longueur L = 5,0 m.
On prendra g = 10 SI ; p~3 ; 2^½ ~1,4.
Initialement le trapéziste B se trouve au point B₀ ( 21 m ; 10,27 m )
Q : A quelle date, ce trapéziste B doit-il s'élancer pour récupérer le trapéziste A au point S ( 20 m ; 10 m) après avoir effectué 2 oscillations?

correction fixe

correction Chimix

---

Oscillateur mécanique, évolution de systèmes : Nantes 2010.

Oscillateur électrique :

L'oscillateur horizontal est constitué d'un ressort en spires non jointives et d'un objet A de masse m.
La constante de raideur du ressort est notée k, et sa longueur non déformé L0.
On appelle G le centre d'inertie de A.
La position de G quand le ressort n'est pas déformé est G0, d'abscisse 0 de l'axe Ox horizontal.
A l'instant de date t quelconque, l'abscisse de G est x.
Les conditions initiales sont représentées par le point P1 de la figure 4.

Dans le cas où les frottements ne sont pas négligeables, on obtient les graphes des figures 3 et 4.
Q :
-Quelle grandeur caractéristique peut-on obtenir de la figure 3 ? Donner sa valeur.
-Identifier les grandeurs physiques correspondant aux courbes c et d. Justifier.
-Construire l'allure de l'énergie cinétique en fonction de x en justifiant par quelques points particuliers.
-Déterminer la valeur de la constante de taideur k à partir de la figure 4. En déduire la masse de l'objet.
-En supposant la force de frottement constante entre P1 et P2, déterminer sa valeur.
-La valeur de la force de frottement reste t-elle la même lors des trajets P1P3 et P3P5 ?


Evolution de systêmes.
Au cours de différentes manipulations, l'expérimentateur a aquis la grandeur x au cours du temps.
Cette grandeur x peut représenter une position d'un solide, la valeur d'une tension électrique par exemple. 
Les graphes sont à la même échelle.

Q : Pour les affirmations suivantes, indiquer si chacune d'elle est fausse, incomplète ou vrai. Justifier.
1. Le système II représente la plus grande vitesse initiale.
2. Le système présente une vitesse nulle à tout instant t>0 s.
3. Aucun système ne voit sa vitesse diminuer au cours du temps.
4. Les graphes I et IV présentent des systèmes dont la vitesse est croissante.
5. L'accélération des solides liés aux systèmes III et IV est nulle pour tout t>0.

Tracé qualitatif d'un graphe.
un véhicule au repos, démarre à la date t=0 s.
Sa vitesse passe de 0 à 25 m/s en 10 s de manière continue à accélération constante.
De la même manière sa vitesse atteint 30 m/s à la date t= 15 s.
Le véhicule cesse d'accélérer et poursuit sa route à cette vitesse pendant 20 s.
Il ralentit ensuite en perdant 5 m/s par seconde durant 5 s jusqu'à subir un violent choc contre un mur.
Echelles imposées : 1,0 cm pour 2,5 s ; 1,0 cm pour 5,0 m/s ; 1,0 cm pour 100 m.
Q : 
 Pour chacun des graphes on précisera quelques valeurs particulières remarquables.
-Tracer le graphe de l'évolution de la vitesse en fonction du temps.
-Tracer le graphe de l'évolution de la vitesse en fonction du temps.


correction fixe
correction chimix

---