Radioactivité, pendule et projectile : concours kiné Berck 2010

Césium 137.
Le césium 137 subit une désintégration ß^- et le noyau fils est le baryum 137. 
Une source radioactive contient une masse m₀ =253 µg de césium 137 à la date t=0. 
On mesure l'activité de cette source à une date t₁ et on obtient la valeur A₁ = 5,67 10⁸ Bq.
On donne N_A = 6,02 10²³ mol^-1 ; 
masse molaire du césium 137 : M = 137 g/mol ; 
demi-vie du césium 137 : t_½ =30,17 années.

Question : Calculer la date t₁ en années. 
15,5 ;
17,8 ;
22,4 ;
25,6 ;
30,2 ;
aucune réponse exacte 





Fission de l'uranium 235
Dans un réacteur nucléaire, l'énergie est produite par la fission de l'uranium 235 sous le choc d'un neutron lent. Le combustible nucléaire utilisé est l'uranium naturel enrichi à 3,4 % en uranium 235 fissile.
Chaque fission d'un noyau d'uranium 235 libère en moyenne une énergie de 200 MeV.
Le rendement de la transformation de l'énergie nucléaire en énergie électrique est de 31 %.
Le réacteur consomme une masse m = 95,9 kg de combustible nucléaire en une journée.
On supposera que tous les noyaux d'uranium 235, contenus dans le combustible, subissent une fission.
On donne : 
masse molaire de l'uranium 235 : M = 235 g/mol ; 1 eV = 1,602 10^-19 J.
Question : Calculer la puissance électrique ( en GW) fournie par ce réacteur.
0,90 ;
0,92 ;
0,94 ;
0,96 ;
0,98 ; 
aucune réponse exacte 




Spectre d'émission
Le spectre d'émission de l'atome de sodium révèle la présence d'un doublet de raies jaunes de longueur d'onde l₁ =589,0 nm et l₂ = 589,6 nm.
Ces deux raies correspondent à une désexcitation de l'atome de sodium, à partir de deux niveaux d'énergie très proches, vers l'état fondamental.
Question : Déterminer l'écart d'énergie ( en meV ) entre ces deux niveaux.
1,2 ;
1,6 ;
2,1 ;
2,4 ;
2,5 ;
aucune réponse exacte


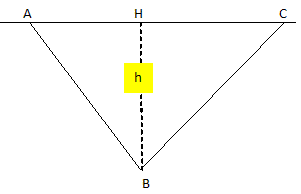
Balise.
Deux bateaux A et C sont séparés l'un de l'autre par une distance de 27 km et ils se trouvent dans le plan vertical contenant la balise.
Le bateau A capte le signal 7,7 s après son émission.
Le bateau C capte le signal de la balise 10,9 s après son émission.
Le son se propage à vitesse constante dans l'eau de mer  : v = 1,5 10³ m/s.
Question : Déterminer la profondeur h ( en km) à laquelle se trouve la balise.
2,3 ;
2,6 ;
2,9 ;
3,2 ;
3,5 ;
aucune réponse exacte

Pendule et projectile.
Masse de la spère : m = 250 g. On lâche la bille en A sans vitesse initiale. 
Quand la bille arrive en B, un dispositif spécifique la décroche du fil et elle continue son mouvement sous la seule action de son poids.
On note S le sommet de la trajectoire de la bille après son décrochage. 
On note P le point de contact avec le sol. 
On néglige l'action de l'air sur la bille dans toutes les phases du mouvement.
Coordonnées des points B et C : x_B =12,2 cm ; y_B =13,4 cm ; x_C =0 cm ; y_C =50,0 cm

Questions : 
Calculer la longueur L du fil constituant le pendule.
Calculer la vitesse en B, notée v_B ( m/s).

Calculer la tension T du fil en B.

Calculer l'ordonnée du sommet SCalculer l'abscisse du point P (en cm).


correction fixe
correction chimix

---

Diagramme des niveaux d'énergie d'un atome : Assas 2010.

On cherche à reconstituer le diagramme de quelques niveaux d'énergie d'un atome X.
On notera 1 le niveau d'énergie fondamental de cet atome.
 Questions :
-Quelle est l'expression de la longueur d'onde l associée à un photon d'énergie E.
-Calculer la valeur de la constante hc en eV nm.
-Quelle est l'expression littérale de DE32, la différence d'énergie entre les niveaux 2 et 3 ?
-Quelle est sa valeur en eV ?
-Quelle est la longueur d'onde l32 correspondant à la transition électronique 3----›2 ?
-Calculer les valeurs des énergies des trois premiers niveaux énergétiques de X.


Correction Chimix
Correction permanente

---

Radioactivité EFOM 2010

Fusion nucléaire deutérium tritium.
On donne les énergies de liaison en MeV par nucléons : 
neutron : 0 ; deutérium  : 1,10 ; tritium : 2,80 ; hélium 4 : 7,10.
La réaction libère :
A- 28,4 MeV. 
B-  17,8 MeV.
C- 10,6 MeV.
D- Cette réaction ne peut se faire qu'après impact d'un neutron sur le tritium. 
E- Cette réaction libère 50 fois plus d'énergie que la fission d'un noyau d'uranium 235. 


Emission de photons.
Un atome émet une radiation de fréquence n lorsqu'il connaît une transition des niveaux d'énergie 3 à 1. 
Ce même atome émet une radiation de fréquence n' lorsqu'il passe du premier état excité au niveau fondamental.
La fréquence de la radiation émise lorsque l'atome passe du niveau d'énergie 3 au niveau d'énergie 2 vaut :
A- n-n'. 
B-  ½(n+n').
C-  ½(n-n'). 
D- n+n'. 
E- autre réponse. 

Famille radioactive.
le plomb ²⁰⁶₈₂Pb est le noyau stable que l'on obtient après une suite de plusieurs désintégrations dont le noyau père est l'uranium ²³⁸₉₂U. 

Les désintégrations sont du type a ou ß. 

Combien en faut-il pour obtenir le plomb 206 ?
A- 10 désintégrations a et 8 désintégrations ß^-. 
B-  8 désintégrations a et 8 désintégrations ß^-.
C-8 désintégrations a et 6 désintégrations ß^-.
D- 8 désintégrations a et 10 désintégrations ß^-.
E- 6 désintégrations a et 10 désintégrations ß^-. 

L'atome d'hydrogène. E_n = -E₀/n².

A- La fréquence d'un photon émis ou absorbé par un atome est reliée aux énergie E_n et E_p de l'atome par la relation de Bohr : DE = |E_p-E_n| = h n = hl/c.  

B- L'énergie d'ionisation de l'atome d'hydrogène est l'énergie minimale qu'il faut fournir à l'atome dans son état fondamental pour arracher l'électron, soit 13,6 eV. 

C- Si l'atome d'hydrogène passe du niveau d'énergie n=5 au niveau n=3 alors la longueur d'onde du photon émis est de l'ordre du micromètre.

D- La radiation émise appartient au domaine de l'infrarouge. 
E- La fréquence du photon absorbé lors de la transition du niveau 3 au niveau 5 est différente  de la fréquence du photon émis lors de la transition inverse.


Courbe d'Aston .
Voici 4 nucléides inconnus X₁, X₂, X₃, X₄ présentés sur la courbe d'Aston :

A- X₁ est plus stable que X₂. 
B- X₂ pourrait être un produit de fission de X₁.
C-  X₃ pourrait être un produit de fission de X₄.
D- L'axe des ordonnées représente l'énergie d'activation.
E- l'axe des ordonnées s'exprime en MeV/nucléon. 

Le produit h c. 
h est la constante de Plank et c la célérité de la lumière dans le vide.
Le produit hc est exprimé en eV nm et il vaut environ :  

10⁰ ; 

10 ;  

10³ ; 

10^-25 ; 

10^-19.



correction fixe
correction chimix

---